What Kind of Free Category is the Controllability Matrix?
by Jade Master
Correction 24/02/25: I have incorrectly claimed that the rank of the horizontal concatenation of matrices is the same as the rank of the diagonal concatenation of matrices defined in this post. It has since been corrected.
I was watching this video about about the controllability matrix, a matrix whose rank tells you whether you’ve supplied enough degrees of freedom to move your control system between any two points. It occured to me that the formula for this matrix looks a lot like the formula for the free enriched category or algebraic path problem (and by the way, these are the same!). First I’ll explain what the controllability matrix is:
The Controllability Matrix
Let A be a square matrix representing a linear ode. This is the standard
\[x' = A x\]Let B be a matrix representing how your control signal transforms to state i.e. so your total control system is modelled by the equation
\[x' = A x + B u\]where $u(t)$ is a vector valued real function. Then the controllability matrix is a sum
\[\mathfrak{C} = B + A B + A^2 B + \ldots + A^n B\]where n is the dimension of A and plus is horizontal concatenation of matrices. Can you spot the free category/algebraic path problem/kleene star/matrix exponential/free monoid yet?
Why this Matrix?
This section is a bit technical and you may feel like skipping it if you don’t feel like getting lost in a mountain of calculus.
The differential equation $x’ = A x + B u$ has a closed form solution.
\[x(t) = \int_{0}^t e^{A(t - \tau)}Bu(\tau)d\tau\]Where $e^{A(t - \tau)}$ is the infinite series
\[\sum_{k=0} ^{\infty} \frac{(t-\tau)^k}{k!} A^k\]A state $\xi$ is reachable if there exists some $t$ with $\xi = x(t)$. We can simplify this condition using the Cayley-Hamilton theorem which says that every matrix satisfies its own eigenvalue equation $a_n A ^n + a_{n-1} A^{n-1} + \ldots + a_0I = 0$. You can take this equation, and solve for $A^n$ as a sum of the lower powers
\[A^{n} = \sum_{i= 0}^{n-1} -a_i A^i\]And furthermore, if you keep multiplying the above equation by $A$ and reducing the right hand side we have:
\[A^{\geq n} = \sum_{i=0}^n c_i A^i\]for some coefficients $c_i$. Not just powers of $A$ but any sum of powers of $A$ can still be expressed as a linear combination of the powers $\leq n$. This applies to the matrix exponential as well! Using this to simplify the matrix exponential in the solution:
\[\begin{align} x(t) & = \int_{0}^t e^{A(t -\tau)}Bu(\tau) \\ & = \int_{0}^t(\sum_{k=0} ^{\infty} \frac{(t-\tau)^k}{k!} A^k)Bu(\tau) \\ & = \int_{0}^t(\sum_{i=0}^n d_i(\tau) A^i )Bu(\tau)\\ & = (\oplus_{i=0}^n A^i B) \cdot \langle \int_0^t d_i (\tau) u_i(\tau) \rangle_{i=1}^n\\ & = \mathfrak{C} \cdot \langle \int_0^t d_i (\tau) u_i(\tau) \rangle_{i=1}^n \\ \end{align}\]Where $\oplus$ denotes horizontal concatenation of matrices. From this equation, you may see that there exists a choice of $u$ such that $x(t) = \xi$ if and only the rank of the contrallability matrix is $n$.
The Wrong Kind of Free Category?
I have shown in The Open Algebraic Path Problem, Prop 1.8 that for a nice enough semiring $R$ that there is an adjunction
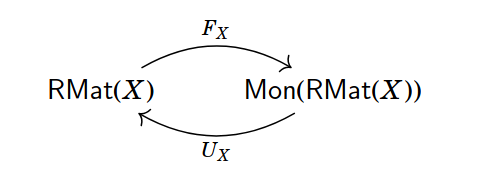
between matrices valued in $R$ and monoids internal to $\mathsf{RMat}(X)$ i.e. $R$-enriched categories. The right adjoint $U_X$ is forgetful and does nothing but forget the monoid structure. The right adjoint $F_X$ finds solutions to the algebraic path problem on $X$. Explicitly,
\[F_X (M) = \sum_{n \geq 0} M^n\]where the sum is the pointwise matrix sum an the product is the usual matrix product using the operations of $R$. Although this sum is infinite, in practice each choice $R$ will have a corresponding principle that allows the computation to stop after a finite number of steps. It is very tempting to notice the similarity between the controllability matrix and $F_X(A) B$ and call it a day. Unfortunately, the universe doesn’t always agree.
This adjunction is not what describes the controllability matrix. The difference is that above, the sum is using the $+$ of $\mathbb{R}$ whereas in the controllability matrix the sum represents horizontal concatenation. There is a different category where this concatenation is close to a coproduct, however there is still a mismatch between this coproduct and the matrix multiplication in the definition of the controllability matrix that I don’t know how to fit into the framework of an adjunction. Mysteries abound! When I posted about this on Mathstodon, Matteo Capucci told me it stinks of higher categories:
Can We Borrow the Coproduct From a Different Category?
Let $\mathsf{Mat}(\mathbb{R})$ be the category of real-valued matrices whose vertex set may vary. In other words,
- the objects are matrices $X \times X \to \mathbb{R}$ or $ Y \times Y \to \mathbb{R}$
- the morphisms functions $f : X \to Y$
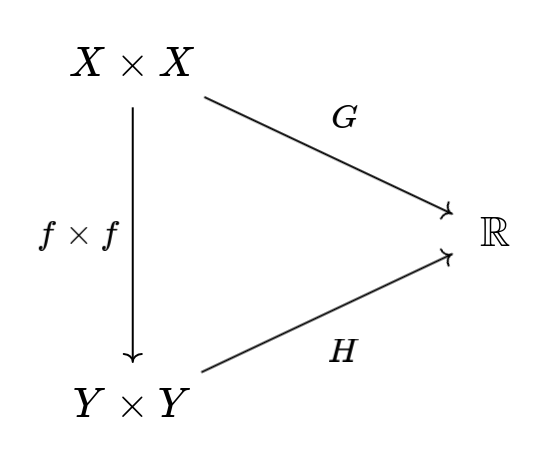
satisfying
\[\forall a, b \in Y \times Y, \sum_{x \in f^{-1} (a), y \in f^{-1}(b)} G(x,y) \leq H(a,b)\]This formula is saying that the pushforward $f_*(G)$ must be less than or equal to $H$.
Proposition: For $\mathbb{R}$-matrices $M$ and $N$, their coproduct $M \oplus N$ in $\mathsf{Mat}(\mathbb{R})$ is the block matrix
\[\begin{bmatrix} M & 0 \\ 0 & N \\ \end{bmatrix}\]where $0$ represents the matrix of appropriate shape with all zeros.
This proposition is almost proven in Lemma 2.5, The Open Algebraic Path Problem. We only need the generalization to the case when $R$ is not necessarily a quantale which I believe should cause no trouble.
Unfortunately, the sum in the controllability matrix still doesn’t match: the controllability matrix uses horizontal concatenation whereas the above is more like diagonal concatenation.
Regardless I am left with more questions than answers. What sort of free category uses a coproduct from a different category than the product? With the help of friends, I hope to report back to this blog with an answer!
tags: